Spectrally Deconfounded Additive Models

Estimate high-dimensional additive models using spectral deconfounding (Scheidegger et al. 2025) . The covariates are expanded into B-spline basis functions. A spectral transformation is used to remove bias arising from hidden confounding and a group lasso objective is minimized to enforce component-wise sparsity. Optimal number of basis functions per component and sparsity penalty are chosen by cross validation.

SDAM(
  formula = NULL,
  data = NULL,
  x = NULL,
  y = NULL,
  Q_type = "trim",
  trim_quantile = 0.5,
  q_hat = 0,
  nfolds = 5,
  cv_method = "1se",
  n_K = 4,
  n_lambda1 = 10,
  n_lambda2 = 20,
  Q_scale = TRUE,
  ind_lin = NULL,
  mc.cores = 1,
  verbose = TRUE,
  notRegularized = NULL
)

Arguments

formula: Object of class formula or describing the model to fit of the form y ~ x1 + x2 + ... where y is a numeric response and x1, x2, ... are vectors of covariates. Interactions are not supported.
data: Training data of class data.frame containing the variables in the model.
x: Matrix of covariates, alternative to formula and data.
y: Vector of responses, alternative to formula and data.
Q_type: Type of deconfounding, one of 'trim', 'pca', 'no_deconfounding'. 'trim' corresponds to the Trim transform (Ćevid et al. 2020) as implemented in the Doubly debiased lasso (Guo et al. 2022) , 'pca' to the PCA transformation(Paul et al. 2008) . See get_Q.
trim_quantile: Quantile for Trim transform, only needed for trim, see get_Q.
q_hat: Assumed confounding dimension, only needed for pca, see get_Q.
nfolds: The number of folds for cross-validation. Default is 5.
cv_method: The method for selecting the regularization parameter during cross-validation. One of "min" (minimum cv-loss) and "1se" (one-standard-error rule) Default is "1se".
n_K: The number of candidate values for the number of basis functions for B-splines. Default is 4.
n_lambda1: The number of candidate values for the regularization parameter in the initial cross-validation step. Default is 10.
n_lambda2: The number of candidate values for the regularization parameter in the second stage of cross-validation (once the optimal number of basis function K is decided, a second stage of cross-validation for the regularization parameter is performed on a finer grid). Default is 20.
Q_scale: Should data be scaled to estimate the spectral transformation? Default is TRUE to not reduce the signal of high variance covariates.
ind_lin: A vector of indices specifying which covariates to model linearly (i.e. not expanded into basis function). Default is `NULL`.
mc.cores: Number of cores to use for parallel processing, if mc.cores > 1 the cross validation is parallelized. Default is `1`. (only supported for unix)
verbose: If TRUE fitting information is shown.
notRegularized: A vector of indices specifying which covariates not to regularize. Default is `NULL`.

Value

An object of class `SDAM` containing the following elements:

X: The original design matrix.
p: The number of covariates in `X`.
var_names: Names of the covariates in the training data.
intercept: The intercept term of the fitted model.
K: A vector of the number of basis functions for each covariate, where 1 corresponds to a linear term. The entries of the vector will mostly by the same, but some entries might be lower if the corresponding component of X contains only few unique values.
breaks: A list of breakpoints used for the B-splines. Used to reconstruct the B-spline basis functions.
coefs: A list of coefficients for the B-spline basis functions for each component.
active: A vector of active covariates that contribute to the model.

References

Ćevid D, Bühlmann P, Meinshausen N (2020). “Spectral Deconfounding via Perturbed Sparse Linear Models.” J. Mach. Learn. Res., 21(1). ISSN 1532-4435, http://jmlr.org/papers/v21/19-545.html.

Guo Z, Ćevid D, Bühlmann P (2022). “Doubly debiased lasso: High-dimensional inference under hidden confounding.” The Annals of Statistics, 50(3). ISSN 0090-5364, doi:10.1214/21-AOS2152 .

Paul D, Bair E, Hastie T, Tibshirani R (2008). ““Preconditioning” for feature selection and regression in high-dimensional problems.” The Annals of Statistics, 36(4). ISSN 0090-5364, doi:10.1214/009053607000000578 .

Scheidegger C, Guo Z, Bühlmann P (2025). “Spectral Deconfounding for High-Dimensional Sparse Additive Models.” ACM / IMS J. Data Sci.. doi:10.1145/3711116 .

Author

Cyrill Scheidegger

Examples

set.seed(1)
X <- matrix(rnorm(10 * 5), ncol = 5)
Y <- sin(X[, 1]) -  X[, 2] + rnorm(10)
model <- SDAM(x = X, y = Y, Q_type = "trim", trim_quantile = 0.5, nfold = 2, n_K = 1)
#> [1] "Initial cross-validation"
#> [1] "Second stage cross-validation"

# if we know that the first covariate one is relevant, we can also choose to not regularize it
model <- SDAM(x = X, y = Y, Q_type = "trim", trim_quantile = 0.5, nfold = 2, 
              n_K = 1, notRegularized = c(1))
#> [1] "Initial cross-validation"
#> [1] "Second stage cross-validation"

# \donttest{
set.seed(22)
library(HDclassif)
#> Loading required package: MASS
data(wine)
names(wine) <- c("class", "alcohol", "malicAcid", "ash", "alcalinityAsh", "magnesium", 
                 "totPhenols", "flavanoids", "nonFlavPhenols", "proanthocyanins", 
                 "colIntens", "hue", "OD", "proline")
wine <- log(wine)

# estimate model
# do not use class in the model and restrict proline to be linear 
model <- SDAM(alcohol ~ . - class, wine, ind_lin = "proline")
#> [1] "Initial cross-validation"
#> [1] "Second stage cross-validation"

# extract variable importance
varImp(model)
#>       malicAcid             ash   alcalinityAsh       magnesium      totPhenols 
#>    2.211114e-06    4.626919e-06    0.000000e+00    0.000000e+00    0.000000e+00 
#>      flavanoids  nonFlavPhenols proanthocyanins       colIntens             hue 
#>    1.000657e-06    3.530140e-06    0.000000e+00    3.331735e-04    0.000000e+00 
#>              OD         proline 
#>    0.000000e+00    0.000000e+00 

# most important variable
mostImp <- names(which.max(varImp(model)))
mostImp
#> [1] "colIntens"

# predict for individual Xj
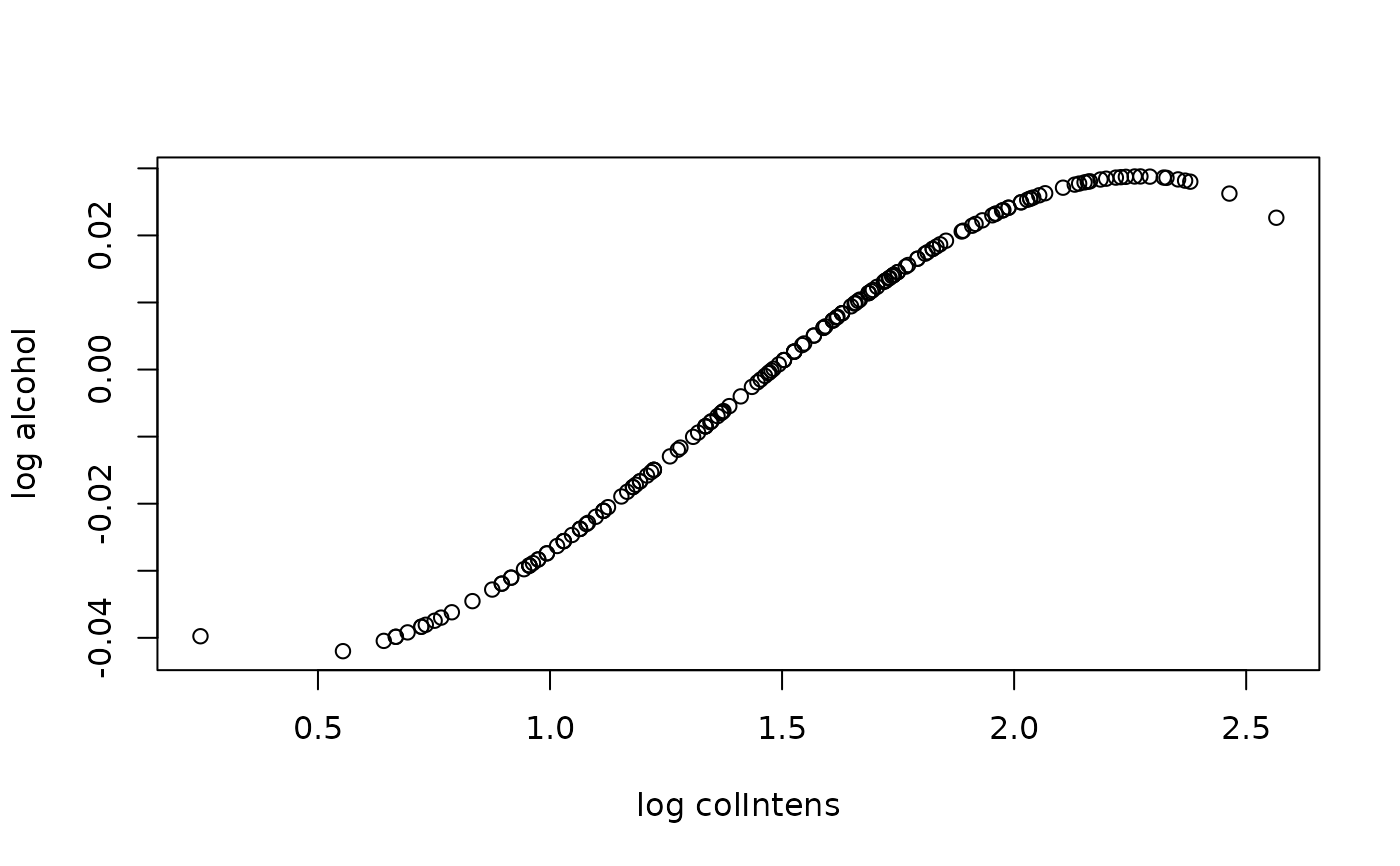
x <- seq(min(wine[, mostImp]), max(wine[, mostImp]), length.out = 100)
predJ <- predict_individual_fj(object = model, j = mostImp, x = x)

plot(x, predJ, 
     xlab = paste0("log ", mostImp), ylab = "log alcohol")


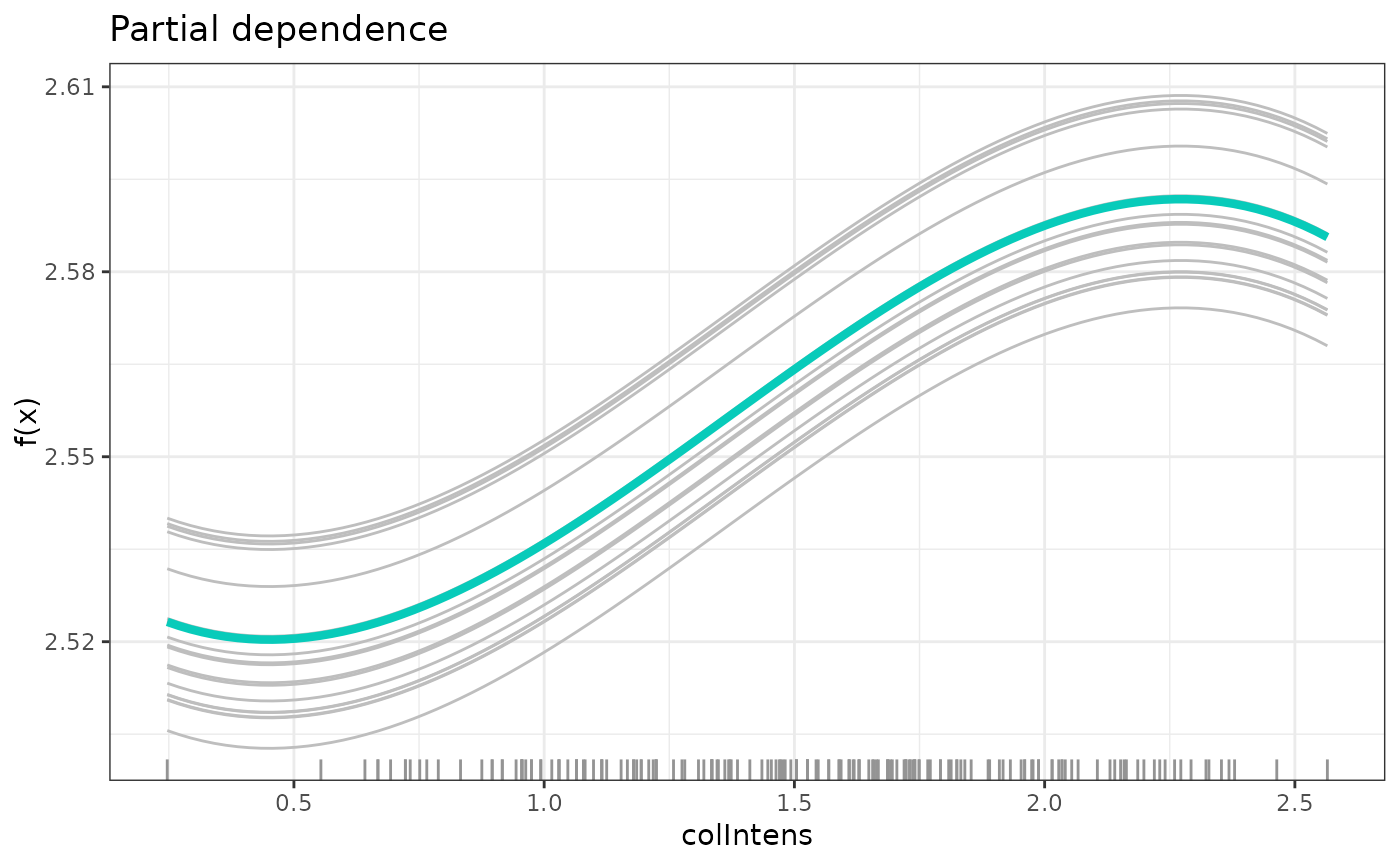
# partial dependece
plot(partDependence(model, mostImp))


# predict 
predict(model, newdata = wine[42, ])
#> [1] 2.56437

## alternative function call
mod_none <- SDAM(x = as.matrix(wine[1:10, -c(1, 2)]), y = wine$alcohol[1:10], 
                 Q_type = "no_deconfounding", nfolds = 2, n_K = 4, 
                 n_lambda1 = 4, n_lambda2 = 8)
#> [1] "Initial cross-validation"
#> [1] "Second stage cross-validation"
# }